[Python] 백준 1991 - 트리 순회

 

실버 I

https://www.acmicpc.net/problem/1991

1991번: 트리 순회

---

📌 문제

이진 트리를 입력받아 전위 순회(preorder traversal), 중위 순회(inorder traversal), 후위 순회(postorder traversal)한 결과를 출력하는 프로그램을 작성하시오.

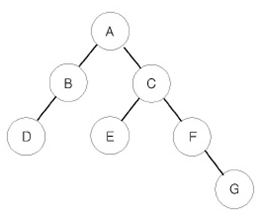
예를 들어 위와 같은 이진 트리가 입력되면,

• 전위 순회한 결과 : ABDCEFG // (루트) (왼쪽 자식) (오른쪽 자식)
• 중위 순회한 결과 : DBAECFG // (왼쪽 자식) (루트) (오른쪽 자식)
• 후위 순회한 결과 : DBEGFCA // (왼쪽 자식) (오른쪽 자식) (루트)

가 된다.

---

📤 입력

 

첫째 줄에는 이진 트리의 노드의 개수 N(1 ≤ N ≤ 26)이 주어진다. 둘째 줄부터 N개의 줄에 걸쳐 각 노드와 그의 왼쪽 자식 노드, 오른쪽 자식 노드가 주어진다. 노드의 이름은 A부터 차례대로 알파벳 대문자로 매겨지며, 항상 A가 루트 노드가 된다. 자식 노드가 없는 경우에는 .으로 표현한다.

---

📥 출력

첫째 줄에 전위 순회, 둘째 줄에 중위 순회, 셋째 줄에 후위 순회한 결과를 출력한다. 각 줄에 N개의 알파벳을 공백 없이 출력하면 된다.

---

💡 접근방식

트리의 특징

- 그래프의 한 종류로, '최소 연결 트리'라고도 불린다.

- 트리는 계층 모델이고, 사이클이 없다.(비순환 그래프)

- 노드가 N개인 트리는 항상 N-1개의 간선(edge)를 가진다.

- 순회의 방법은 preorder(전위순회), inorder(중위순회), postorder(후위순회)가 있다. 

(위 사진의 용어는 맨 아래 두 번째 블로그 참고!)

 

전위 순회는 [루트 - 왼쪽 자식 - 오른쪽 자식] 순으로 순회

중위 순회는 [왼쪽 자식 - 루트 - 오른쪽 자식] 순으로 순회

후위 순회는 [왼쪽 자식 - 오른쪽 자식 - 루트] 순으로 순회

---

💻 코드

# https://www.acmicpc.net/problem/1991
# 트리 순회

N = int(input())
tree = {}
 
for n in range(N):
    root, left, right = input().split()
    # 트리 구조를 표현하는 방법
    tree[root] = [left, right]
 
# 전위순회
def preorder(root):
    if root != '.':
        print(root, end='')  # root
        preorder(tree[root][0])  # left
        preorder(tree[root][1])  # right
 
# 중위 순회 
def inorder(root):
    if root != '.':
        inorder(tree[root][0])  # left
        print(root, end='')  # root
        inorder(tree[root][1])  # right
 
# 후위 순회 
def postorder(root):
    if root != '.':
        postorder(tree[root][0])  # left
        postorder(tree[root][1])  # right
        print(root, end='')  # root
 
 
preorder('A')
print()
inorder('A')
print()
postorder('A')

 

---

📝 NOTE

참고한 블로그들

https://velog.io/@ohk9134/%EB%B0%B1%EC%A4%80-1991%EB%B2%88-%ED%8A%B8%EB%A6%AC-%EC%88%9C%ED%9A%8C-python-%ED%8A%B8%EB%A6%AC-%EA%B5%AC%ED%98%84

백준 1991번 - 트리 순회 / python 트리 구현

https://gmlwjd9405.github.io/2018/08/12/data-structure-tree.html

[자료구조] 트리(Tree)란 - Heee's Development Blog

https://withhamit.tistory.com/282

트리 순회(전위 순회, 중위 순회, 후위 순회)